Law of Total Probability

This can be intuitively thought of as the partition of the whole space yielding a partition of $A$:

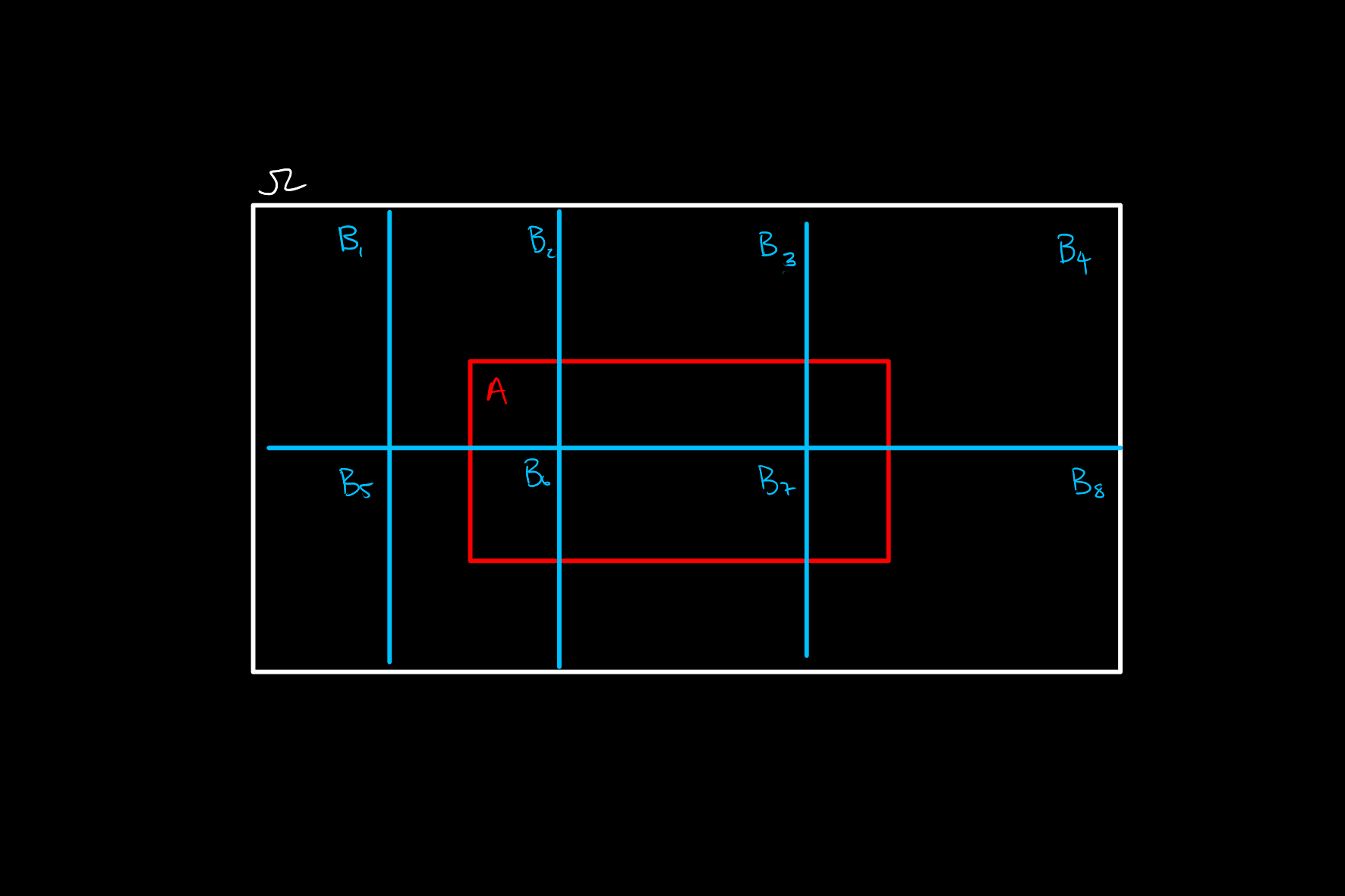
and then the probability of $A$ calculated by summing the part in each set within the partition

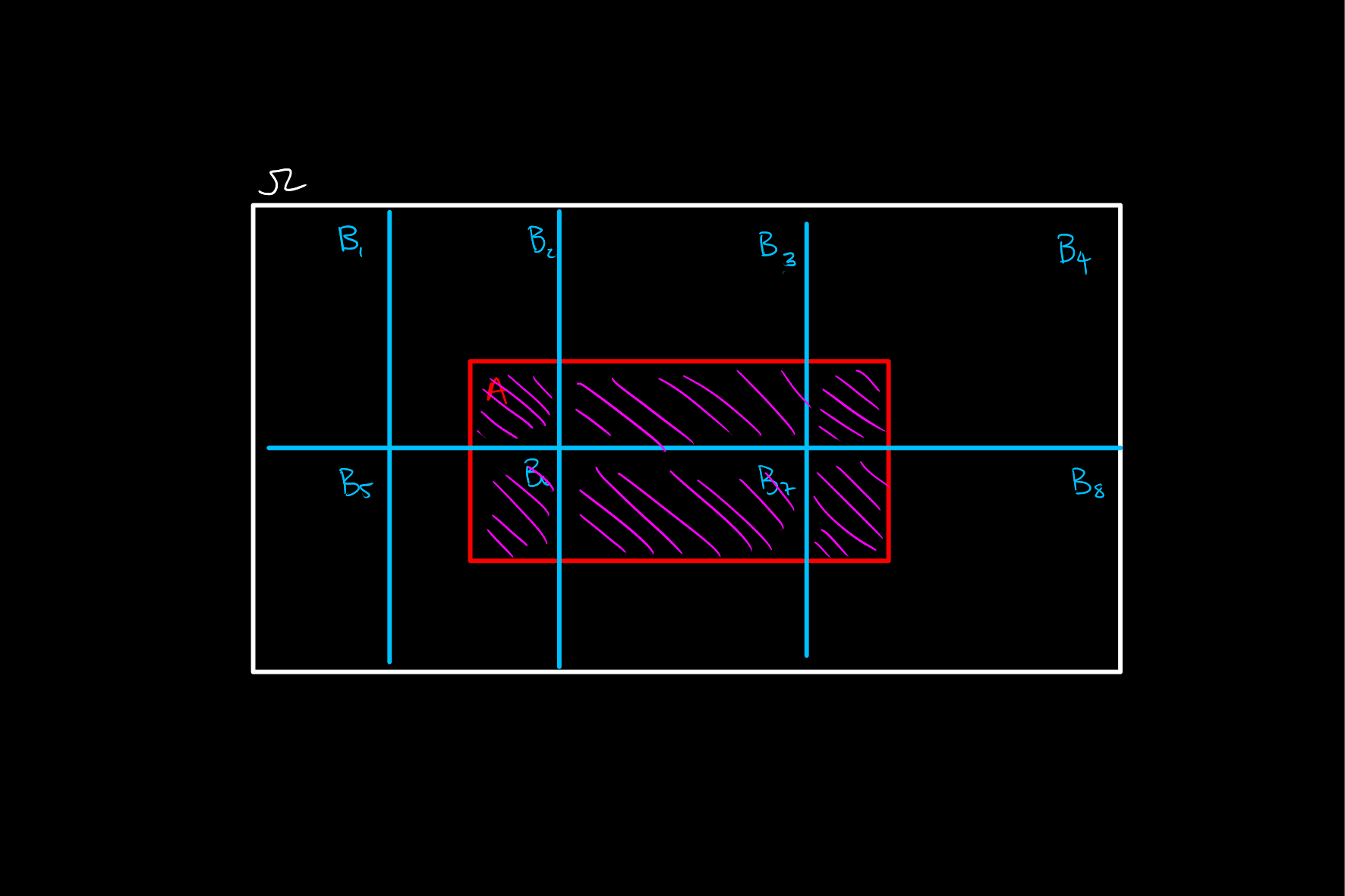
Proof

The result follows very simply from the ability to split the measure across a disjoint union:

and hence, the result we must prove that $A\cap B_i$ and $A\cap B_j$ are disjoint for $i\ne j$.

This is because:

where $B_i\cap B_j=\varnothing$ from the assumption that $\{B_i{\}}_{i=1}^n$ partitions the sample space.